这篇文章上次修改于 473 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

本文共 1261 个字，阅读时长 ≈ 4 分钟

题目链接

这是一道隐藏的很深的结论题好像只是因为我太弱，我一开始看时以为是个模拟，然后看到数据范围之后我傻了。
怎么办呢？我们要坚信暴力出奇迹，打表出省一画图可以解决一切问题。

于是这个图就出来了

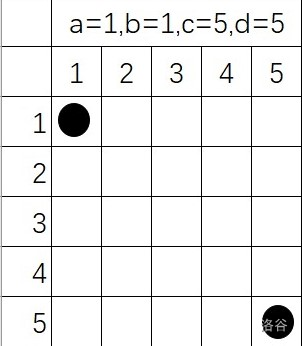
然后根据玄学手推可以推出最短路是这个样子的

由此我们可以得到一种情况，也就是当a=b且c=d时两点间的最短路为两点的曼哈顿距离，公式为$|x_1-x_2|+|y_1-y_2|$。敲黑板！曼哈顿距离是本题解题的关键

但是毒瘤大犇出题人怎么可能这么轻易地就放过我们呢。

于是我们可以通过第一种情况延伸出剩下两种情况

abcd形成一个长方形的

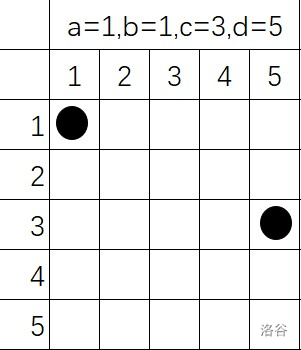
a=c的（Subtask2）

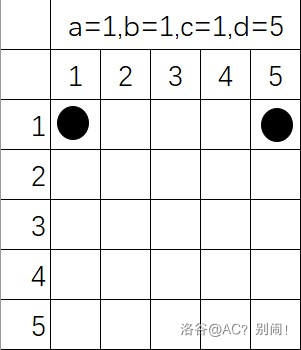
这里就会有人问了，诶诶你不是说从第一个延伸出来的吗，怎么看着跟第一个一点关系都没有呢？不要着急，等我把这两种情况的最短路画出来你就知道了

第二种情况

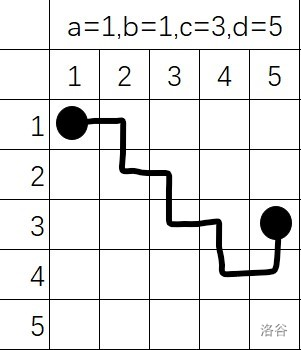
第三种情况

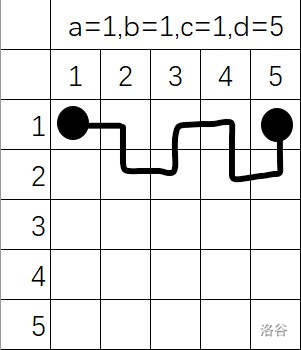
我们可以把第二种情况看做先把cd所在的那一行当成正方形的底，然后走一遍情况一，再直走走到点cd

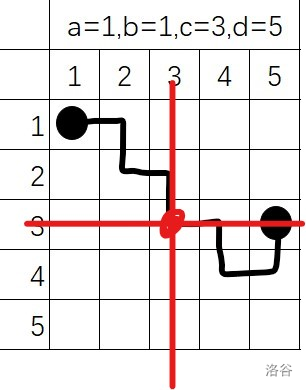
直走我们用的方法是这个样子的，因为题目要求不能连续往同一个方向走，而这样走可以被证明每一步是最短的

按这样直走，我们可以算出直走所需要的的步数，但是这里需要分类讨论（此处为本题巨坑，本蒟蒻卡在这里调了两个多小时），一种是两点的距离为偶数，一种是两点的距离是奇数。

两点的距离是偶数时，步数为两点的距离乘以二，因为每走一步之后需要重置方向，要往上或往下再走一步。

两点的距离是奇数时，步数为两点的距离乘以二减一，因为走最后一步时不需要再重置方向了，所以要减去多的一步（斜线划分步数）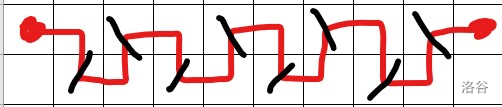

因为当我们从点ab走到正方形的右下角时，正方形的右下角和点cd在一条横轴上，所以我们直接走直线即可到达点cd，所需的步数即为从点ab走到正方形右下角的步数加从正方形右下角走直线到点cd的步数。

而情况三则比较简单，直接从点ab走直线到点cd即可。

本题最大的难点在于分类讨论和三种情况的解决，都解决后其实就是一道结论题

AC代码

#include<iostream>
#include<cstdio>
#include<cmath>
#define int long long//反正空间够，不开long long见祖宗，而且你必须开
using namespace std;
signed main()//因为define了int，所以要改成signed
{
    int T;
    cin>>T;
    for(int cishu=0;cishu<T;++cishu){
        int a,b,c,d;
        cin>>a>>b>>c>>d;
        int ac=abs(a-c),bd=abs(b-d);
        int temp=ac,ans=min(ac,bd);
       //哪边小把哪边当做正方形的底，要不然就把点cd越过去了
        ac-=min(temp,bd);//求需要直走的长度
      bd-=min(temp,bd);
        int bigger=max(ac,bd);
        if(bigger&1) cout<<(ans*2+bigger*2-1);
      //位运算判断奇偶更快
        else cout<<(ans*2+bigger*2);
        cout<<endl;
    }
    return 0;
}