这篇文章上次修改于 454 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

本文共 2549 个字，阅读时长 ≈ 7 分钟

P2216 [HAOI2007]理想的正方形

这是一道很好的二维单调队列/二维ST表练习题

题意

给你一个 $a \times b$ 的矩阵，从中找出一个 $n \times n$ 的矩阵，使这个小矩阵中最大值和最小值的差值最小，$n$ 是输入给出的。

样例

输入

5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2

输出

1

我们看到一道题先想想暴力怎么做，然后想优化。这道题第一眼就是暴力枚举小矩阵（就是 $n \times n$ 的矩阵），然后去找矩阵中最大和最小值。找最大最小值这个操作很容易想到可以用ST表解决，有了 $n$ 的范围之后也可以用单调队列，我不太会二维ST表所以就用单调队列了。

二维单调队列的实现个人感觉挺暴力的，我们对大矩阵每行跑一遍滑动窗口，对每一次滑动找出最大最小值，最大值存在二维数组 $xa\left[ \right]\left[ \right]$ 中，最小值存在二维数组 $xi\left[\right]\left[\right]$ 中，那这样的话 $xa\left[ i \right]\left[ j \right]$ 就表示第 $i$ 行第 $j\sim j+k-1$ 列中最大的值，$xi\left[ i \right]\left[ j \right]$ 就表示第 $i$ 行第 $j\sim j+k-1$ 列中最小的值。这样每一行的最大最小值我们找出来了，我们再对找出来的每行的最大最小值这两个二维数组每列跑一遍滑动窗口，这样就能把每 $n$ 行每 $n$ 列的最大最小值综合起来，就能找出每个 $n \times n$ 矩阵的最大最小值。我们把这个矩阵的最大值存到 $ya\left[\right]\left[\right]$ 中，$ya\left[i \right]\left[j \right]$ 表示以 $\left(i,j\right)$ 为左上角的边长为 $n$ 的正方形中的最大值，$yi\left[\right]\left[\right]$ 则存的是最小值。

我说的估计不好理解，这里拿样例画个图解释一下。

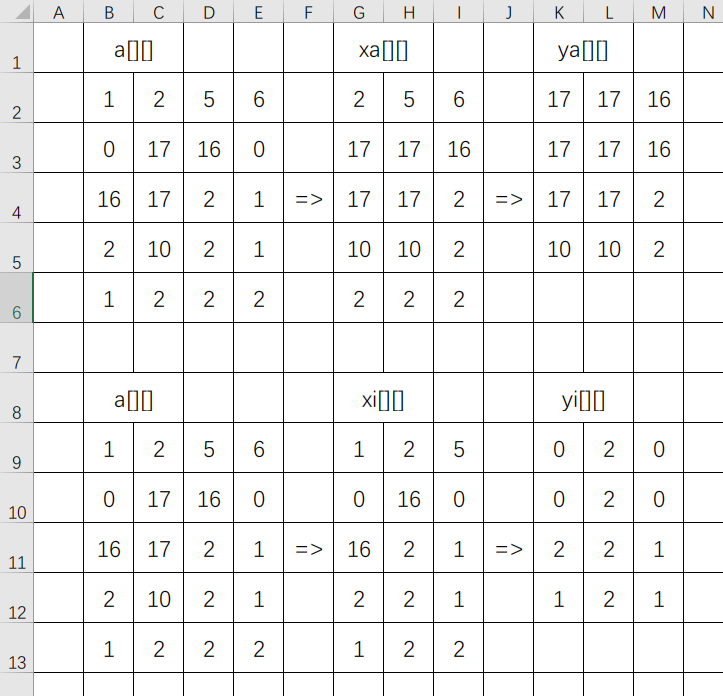
我们可以感性理解一下，将 $a$ 数组转化成 $xa$ 和 $xi$ 数组的步骤就相当于是把 $a$ 数组的 $n$ 列缩成了一列，并把找到的最值存在数组里，然后转化成 $ya$ 和 $yi$ 数组的这一步就是把 $xa$ 和 $xi$ 数组的n行缩成了一行，并把找到的最值存在数组里。因为 $ya$ 和 $yi$ 数组存储的是按行找到的最值又按列找了一遍，这样就综合成了一个矩阵的最值。既然矩阵的最值都已经找完了，剩下的就剩枚举矩阵找最小值了。上代码

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#ifdef ONLINE_JUDGE
#define debug(x)
#else
#define debug(x) cout<<' '<<#x<<'='<<x<<endl;
#endif
using namespace std;
inline int read(){
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-') f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<3)+(x<<1)+(c^48);
        c=getchar();
    }
    return x*f;
}
inline void write(int x){
    if(x<0){x=-x;putchar('-');}
    if(x>9) write(x/10);
    putchar(x%10+'0');
}//快读快写不解释
const int maxn=1003;
//n，m，k是题目中的a，b，d
//ha，ta是最大值单调队列的head，tail
//hi，ti是最小值单调队列的head，tail
int n,m,k,ha,ta,hi,ti;
int qa[maxn],qi[maxn];//单调队列
//a数组是原值，其他跟上面讲的一样
int a[maxn][maxn],xa[maxn][maxn],xi[maxn][maxn],ya[maxn][maxn],yi[maxn][maxn];
int main()
{
    n=read();m=read();k=read();
    for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) a[i][j]=read();
    for(int i=1;i<=n;++i){//按行找最大最小值
        ha=hi=ta=ti=0;//多用不清空，爆零两行泪
        for(int j=1;j<=m;++j){
            //最大值单调队列
            while(ha<ta&&qa[ha]<=j-k) ha++;
            while(ha<ta&&a[i][qa[ta-1]]<a[i][j]) ta--;
            //最小值单调队列
            while(hi<ti&&qi[hi]<=j-k) hi++;
            while(hi<ti&&a[i][qi[ti-1]]>a[i][j]) ti--;
            qa[ta++]=j;
            qi[ti++]=j;
            if(j>=k) xa[i][j-k+1]=a[i][qa[ha]],xi[i][j-k+1]=a[i][qi[hi]];
        }
    }
    for(int i=1;i<=m-k+1;++i){//按列找最大最小值
        ha=ta=hi=ti=0;
        for(int j=1;j<=n;++j){
            while(ha<ta&&qa[ha]<=j-k) ha++;
            while(hi<ti&&qi[hi]<=j-k) hi++;
            while(ha<ta&&xa[qa[ta-1]][i]<xa[j][i]) ta--;
            while(hi<ti&&xi[qi[ti-1]][i]>xi[j][i]) ti--;
            qa[ta++]=j;
            qi[ti++]=j;
            if(j>=k) ya[j-k+1][i]=xa[qa[ha]][i],yi[j-k+1][i]=xi[qi[hi]][i];
        }
    }
    int ans=1000000009;
    //注意范围，缩完之后行数和列数变少了
    for(int i=1;i+k-1<=n;++i){
        for(int j=1;j+k-1<=m;++j){
            ans=min(ans,ya[i][j]-yi[i][j]);
        }
    }
    write(ans);
    putchar('\n');
    return 0;
}